A System Of Equations Has Infinitely Many Solutions When
A system of equations has infinitely many solutions when. 1 0 0 2 1 0 0 1 0 3. Y x 3. As you can see the final row of the row reduced matrix consists of 0.
True or false. The two lines representing the system are intersecting the two lines representing the system are parallel. A system of linear equations can have no solution a unique solution or infinitely many solutions.
Of course this has little to do with the numbers 3 and 4 beyond the fact that 3 4. In simpler words we can say that if the two lines are sharing the same line then the system would result in an infinite solution. _____It is possible for a system of 3 linear equations with 5 variables to have a unique solution.
C True or FalseIf the system Amathbfxmathbfb has a unique solution then A must be a square matrix. Two systems of equations are given below for each system choose the best description of it solution. Lets use python and see what answer we get.
For example consider the following equations. If a system of linear equations has infinitely many solutions then the system is called ____. The first one the rows are independent and thus any equations using it will have one unique solution.
So first my brain just wants to simplify this left-hand side a little bit and then think about how I can engineer the right-hand side so its going to be the same as the left no matter what x I pick. Show graphically that each one of the following systems of equations has infinitely many solutions. A linear system with fewer equations than unknowns must have infinitely many solutions.
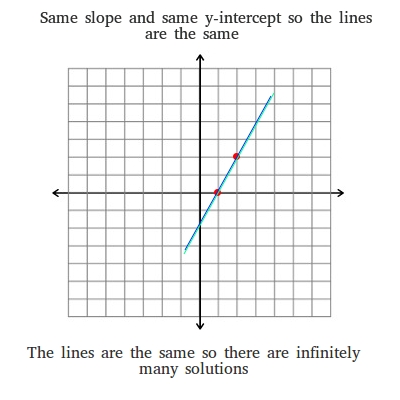
5y 5x 15. If a 1 a 2 b 1 b 2 c 1 c 2 then there will be infinitely many solutions.
A system of linear equations can have no solution a unique solution or infinitely many solutions.
If the number of rows of a matrix is less than the number of columns then the matrix must have a non-trivial null space and so solutions to A x b when they exist cannot be unique. If A x b has a solution it will always have infinitely many solutions. 1 the system has no solution 2 the system has a unique solution 3 the system has a infinitity many solutions. _____It is possible for a system of 3 linear equations with 5 variables to have a unique solution. __F___ Whenever a system of linear equations has free variables the system has infinitely many solutions. Linear System of Equations with Infinitely Many Solutions - YouTube. For a system of equations a 1 x b 1 y c 1 0. How many solutions does the following system of linear equations have and I have my system right over here theres a couple of ways to think about it one way is to think about them graphically and think about well are they the same line in which case they would have an infinite number of solutions are they parallel in which case they never intersect youd have no solutions or do they intersect. The first one the rows are independent and thus any equations using it will have one unique solution.
True or false. So first my brain just wants to simplify this left-hand side a little bit and then think about how I can engineer the right-hand side so its going to be the same as the left no matter what x I pick. The second 123235 358 so they are dependent. X - 2y 11 0 3x - 6y 33 0 asked Apr 26 in Linear Equations by Haifa 242k points pair of linear equations in two variables. As you can see the final row of the row reduced matrix consists of 0. _____It is possible for a system of 3 linear equations with 5 variables to have a unique solution. A system has infinitely many solutions when it is consistent and the number of variables is more than the number of nonzero rows in the rref of the matrix.

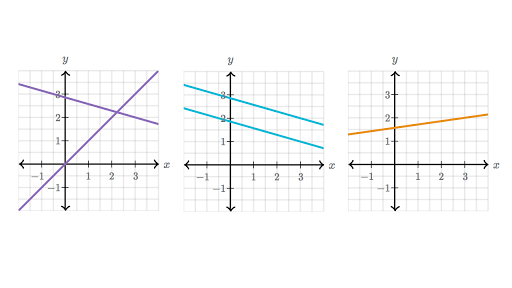
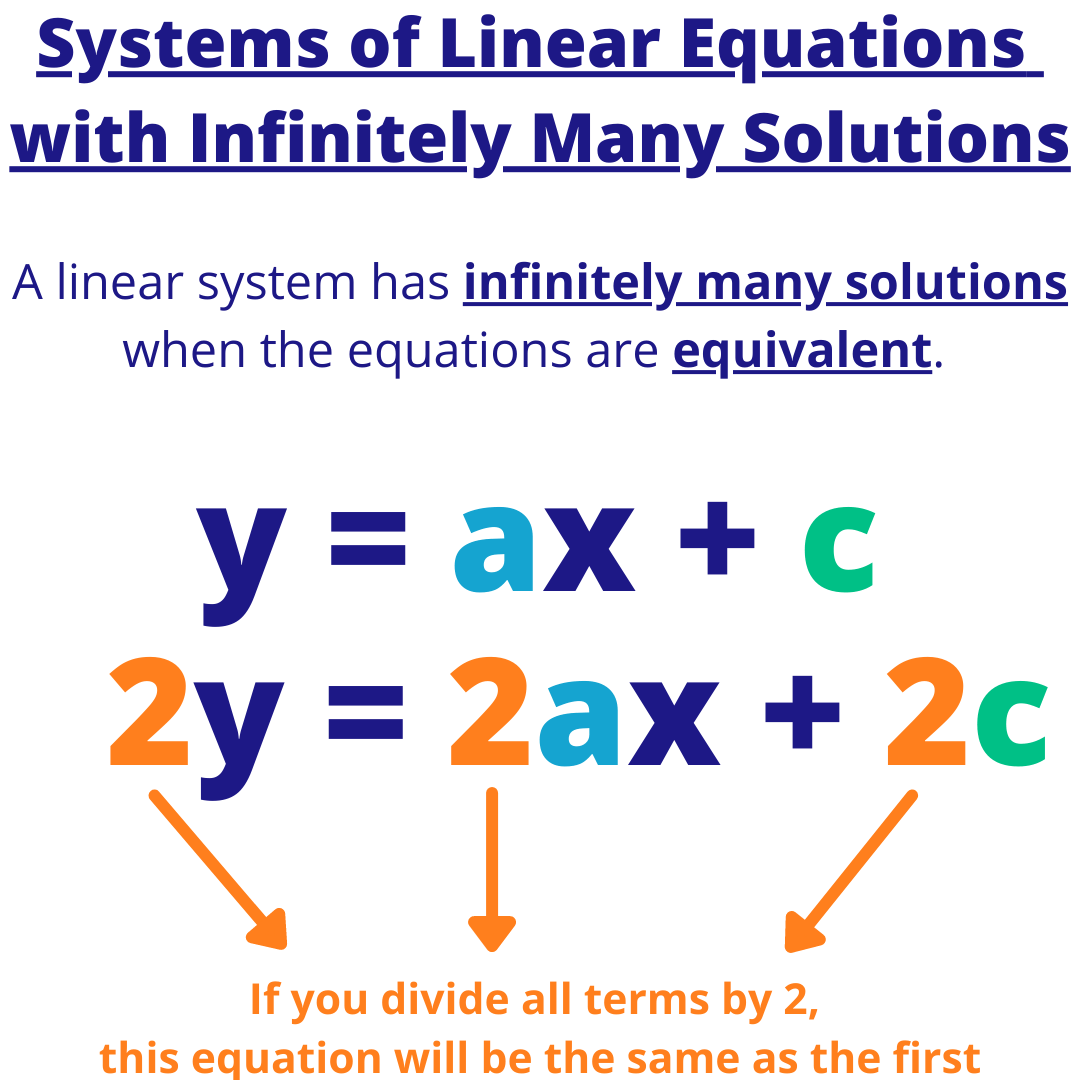

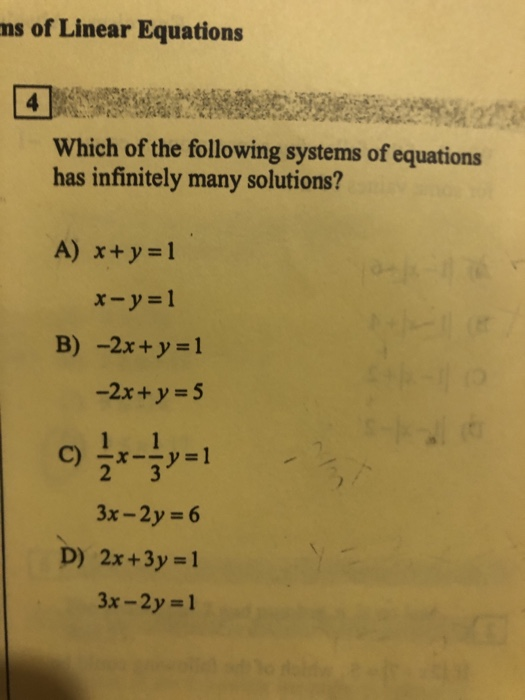











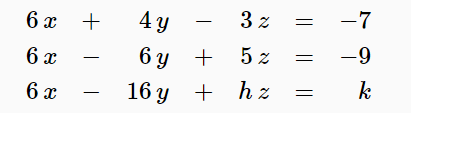



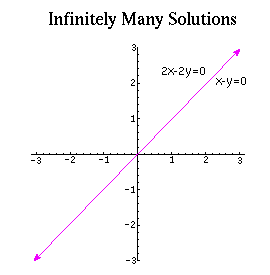


















Posting Komentar untuk "A System Of Equations Has Infinitely Many Solutions When"